Gaussian Mixture Models in R

Gaussian mixture models (GMMs) are widely used for modelling stochastic problems. Indeed, a wide diversity of packages have been developed in R. However, no recent review describing the main features offered by these packages and comparing their performances has been performed. In this article, we first introduce GMMs and the EM algorithm used to retrieve the parameters of the model and analyse the main features implemented among seven of the most widely used R packages. We then empirically compare their statistical and computational performances in relation with the choice of the initialisation algorithm and the complexity of the mixture. We demonstrate that the best estimation with well-separated components or with a small number of components with distinguishable modes is obtained with REBMIX initialisation, implemented in the rebmix package, while the best estimation with highly overlapping components is obtained with k-means or random initialisation. Importantly, we show that implementation details in the EM algorithm yield differences in the parameters’ estimation. Especially, packages mixtools (Young et al. 2020) and Rmixmod (Langrognet et al. 2021) estimate the parameters of the mixture with smaller bias, while the RMSE and variability of the estimates is smaller with packages bgmm (Ewa Szczurek 2021) , EMCluster (W.-C. Chen and Maitra 2022) , GMKMcharlie (Liu 2021), flexmix (Gruen and Leisch 2022) and mclust (Fraley, Raftery, and Scrucca 2022). The comparison of these packages provides R users with useful recommendations for improving the computational and statistical performance of their clustering and for identifying common deficiencies. Additionally, we propose several improvements in the development of a future, unified mixture model package.

Bastien Chassagnol (Laboratoire de Probabilités, Statistiques et Modélisation (LPSM), UMR CNRS 8001) , Antoine Bichat (Les Laboratoires Servier) , Cheïma Boudjeniba (Systems Biology Group, Dept. of Computational Biology, Institut Pasteur) , Pierre-Henri Wuillemin (Laboratoire d’Informatique de Paris 6 (LIP6), UMR 7606) , Mickaël Guedj (Les Laboratoires Servier) , David Gohel (ArData) , Gregory Nuel (Laboratoire de Probabilités, Statistiques et Modélisation (LPSM), UMR CNRS 8001) , Etienne Becht (Les Laboratoires Servier)
2023-11-01

1 Introduction to Mixture modelling

Formally, let’s consider a pair of random variables \((X,S)\) with \(S \in \{1, \ldots, k\}\) a discrete variable and designing the component identity of each observation. When observed, \(S\) is generally denoted as the labels of the individual observations. \(k\) is the number of mixture components. Then, the density distribution of \(X\) is given in Equation (1):

\[\begin{equation} \begin{split} f_\theta(X) &= \sum_S f_\theta (X, S) \\ &= \sum_{j=1}^k p_j f_{\zeta j}(X), \quad X\in\mathbb{R} \end{split} \tag{1} \end{equation}\]

where \(\theta = (p, \zeta) = (p_1, \ldots, p_k, \zeta_1, \ldots, \zeta_k)\) denotes the parameters of the model: \(p_j\) is the proportion of component \(j\) and \(\zeta_j\) represents the parameters of the density distribution followed by component \(j\). In addition, since \(S\) is a categorical variable parametrized by \(p\), the prior weights must enforce the unit simplex constraint (Equation (2)):

\[\begin{equation} \begin{cases} p_j \ge 0 \quad \forall j \in \{1, \ldots, k \}\\ \sum_{j=1}^k p_j =1 \end{cases} \tag{2} \end{equation}\]

In terms of applications, mixture models can be used to achieve the following goals:

\[\begin{equation} \eta_{i} (j) := \mathbb{P}_{\theta} (S_i=j |X_i=x_i) \tag{3} \end{equation}\]

In section Univariate and multivariate Gaussian distributions in the context of mixture models, we describe the most commonly used family, the Gaussian Mixture Model (GMM). We then present the MLE estimation of the parameters of a GMM, introducing the classic EM algorithm in section Parameter estimation in finite mixtures models. Finally, we introduce bootstrap methods used to evaluate the quality of the estimation and metrics used for the selection of the best model in respectively appendices Derivation of confidence intervals in GMMs and Model selection.

1.1 Univariate and multivariate Gaussian distributions in the context of mixture models

We focus our study on the finite Gaussian mixture models (GMM) in which we suppose that each of the \(k\) components follows a Gaussian distribution.

We recall below the definition of the Gaussian distribution in both univariate and multivariate context. In the finite univariate Gaussian mixture model, the distribution of each component \(f_{\zeta j}(X)\) is given by the following univariate Gaussian p.d.f. (probability density function) (Equation (4)):

\[\begin{equation} f_{\zeta j}(X=x)=\varphi_{\zeta_j}(x | \mu_j, \sigma_j):=\frac{1}{\sqrt{2\pi} \sigma_j} \exp^{- \frac{(x - \mu_j)^2}{2 \sigma_j^2}} \tag{4} \end{equation}\] which we note: \(X \sim \mathcal{N}(\mu_j, \sigma_j)\).

In the univariate case, the parameters to be inferred from each component, \(\zeta_j\), are: \(\mu_j\), the location parameter (equal to the mean of the distribution) and \(\sigma_j\), the scale parameter (equal to the standard deviation of the distribution with a Gaussian distribution).

Following parsimonious parametrisations with respect to univariate GMMs are often considered:

In the finite multivariate Gaussian mixture model, the distribution \(f_{\zeta j}(\boldsymbol{X})\) of each component \(j\), where \(\boldsymbol{X} \in \mathbb{R}^D =(X_1, \ldots, X_D)^\top\) is a multivariate random variable of dimension \(D\), is given by the following multivariate Gaussian p.d.f. (Equation (5)):

\[\begin{equation} f_{\zeta j}(\boldsymbol{X}=\boldsymbol{x})=\operatorname{det}(2\pi\boldsymbol{\Sigma}_j)^{-\frac{1}{2}} \exp\left( -\frac{1}{2} (\boldsymbol{x} - \boldsymbol{\mu}_j) \boldsymbol{\Sigma}_j^{-1} (\boldsymbol{x} - \boldsymbol{\mu}_j)^\top\right) \tag{5} \end{equation}\]

which we note \(\boldsymbol{X} \sim \mathcal{N}_D(\boldsymbol{\mu}_j, \boldsymbol{\Sigma}_j)\). The parameters to be estimated for each component can be decomposed into:

Three families of multivariate GMMs are often considered:

In the multivariate setting, the volume, shape, and orientation of the covariances can be constrained to be equal or variable across clusters, generating 14 possible parametrisations with different geometric characteristics (Celeux and Govaert 1992; Banfield and Raftery 1993). We review them in Appendix Parameters estimation in a high-dimensional context and Table 5. Of note, the correlation matrix can be easily derived from the covariance matrix with the following normalisation: \(\operatorname{cor}(\boldsymbol{X})=\left(\frac{\operatorname{cov}(x_l, x_m)}{\sqrt{\operatorname{var}(x_l)} \times \sqrt{\operatorname{var}(x_m)}}\right)_{(l,m) \in D \times D}\). Correlation if strictly included between -1 and 1, the strength of the correlation is given by its absolute value while the type of the interaction is returned by its sign. A correlation of 1 or -1 between two features indicates a strictly linear relationship.

For the sake of simplicity and tractability, we will only consider the fully unconstrained model in both the univariate (heteroscedastic and unbalanced classes) and multivariate dimension (unbalanced and complete covariance matrices for each cluster) in the remainder of our paper.

1.2 Parameter estimation in finite mixtures models

A common way for estimating the parameters of a parametric distribution is the maximum likelihood estimation (MLE) method. It consists in estimating the parameters by maximising the likelihood, or equivalently the log-likelihood of a sample. In what follows, \(\ell(\theta|x_{1:n})=\log (f(x_{1:n}|\theta))\) is the log-likelihood of a n-sample. When all observations are independent, it simplifies to \(\ell(\theta|x_{1:n}) = \sum_{i=1}^n \log (f(x_i|\theta))\). The MLE consists in finding the parameter estimate \(\hat{\theta}\) which maximises the log-likelihood \(\hat{\theta} = \arg \max \ell (\theta | x_{1:n})\).

Recovering the maximum of a function is generally performed by finding the values at which its derivative vanishes. The MLE in GMMs has interesting properties, as opposed to the moment estimation method: it is a consistent, asymptotically efficient and unbiased estimator (McLachlan and Peel 2000; Chen 2016).

When \(S\) is completely observed, for pairs of observations \((x_{1:n}, s_{1:n})\), the log-likelihood of a finite mixture model is simply given by Equation (6):

\[\begin{equation} \ell(\theta|X_{1:n}=x_{1:n}, S_{1:n}=s_{1:n})=\sum_{i=1}^n \sum_{j=1}^k \left[\log\left(f_{\zeta_j} (x_i, s_i=j)\right) + \log(p_j) \right]_{\mathbf{1}_{s_i=j}} \tag{6} \end{equation}\]

where an analytical solution can be computed provided that a closed-form estimate exists to retrieve the parameters \(\zeta_j\) for each components’ parametric distribution. The MLE maximisation, in this context, involves the estimation of the parameters for each cluster, denoted as \(\zeta_j\). The corresponding proportions, \(p_j\), can be straightforwardly computed as the ratios of observations assigned to cluster \(j\) relative to the total number of observations, \(n\).

However, when \(S\) is unobserved, the log-likelihood, qualified as incomplete with respect to the previous case, is given by Equation (7):

\[\begin{equation} \ell (\theta \vert x_{1:n}) = \sum_{i=1}^n \log \left( \underbrace{\sum_{j=1}^k p_j f_{\zeta_j}(x_i)}_{\text{sum of of logs}} \right) \tag{7} \end{equation}\]

The sum of terms embed in the log function (see underbrace section in Equation (7)) makes it intractable in practice to derive the null values of its corresponding derivative. Thus, no closed form of the MLE is available, including for the basic univariate GMM model. This is why most parameter estimation methods derive instead from the EM algorithm, first described in Dempster et al. (1977). We describe its main theoretical properties, the reasons for its popularity, and its main limitations in the next section.

1.3 The EM algorithm

In cases where both \(S\) and the parameters associated to each cluster are unknown, there is no available closed-form solution that would jointly maximise the log-likelihood, as defined in Equation (7), with respect to the set of parameters \(({\theta}, S)\). However, when either \(S\) or \(\theta\) are known, the estimation of the other parameters is straightforward. Hence, the general principle of EM-like algorithms is splitting this complex non-closed joint MLE estimation of \((S, \theta)\) into the iterative estimation of \(S_q\) from \(\hat{\theta}_{q-1}\) and \(X\) (expectation phase, or E-step of the algorithm) and the estimation of \(\hat{\theta}_{q}\) from \((S_q\) and \(X\) (maximisation phase, or M-step), with \(\hat{\theta}_{q-1}\) being the estimated parameters at the previous step \(q-1\), until we reach the convergence.

The EM algorithm sets itself apart from other commonly used methods by taking into account all possible values taken by the latent variable \(S\). To do so, it computes the expected value of the log likelihood of \(\theta\), conditioned by the posterior distribution \(\mathbb{P}_{\hat{\theta}_{q-1}} (S|X)\), also named as the auxiliary function. Utilising the assumption of independence among observations in a mixture model, the general formula of this proxy function of the incomplete log-likelihood is given in finite mixture models by Equation (8).

\[\begin{equation} \begin{split} Q(\theta|\hat{\theta}_{q-1}) & := \mathbb{E}_{S_{1:n}| X_{1:n}, \hat{\theta}_{q-1}} \left[\ell(\theta | X_{1:n}, S_{1:n})\right] \\ &=\sum_{i=1}^n \sum_{j=1}^k \eta_{i}(j) \left( \log (p_j) + \log (\mathbb{P}(X_i|S_i=j, \theta)) \right) \end{split} \tag{8} \end{equation}\]

with \(\hat{\theta}_{q-1}=\hat{\theta}\) the current estimated parameter value.

In practice, the EM algorithm consists in performing alternatively E-step and M-step until convergence, as described in the pseudocode below (Box 1):

  • step E: determine the posterior probability function \(\eta_i(j)\) for each observation of \(X\) for each possible discrete latent class, using the initial estimates \(\hat{\theta}_0\) at step \(q=0\), or the previously computed estimates \(\hat{\theta}_{q-1}\). The general formula is given by Equation (9):
\[\begin{equation} \eta_i(j) = \frac{p_j f_{\zeta_j} (x_i)}{\sum_{j=1}^k p_j f_{\zeta_j} (x_i)} \tag{9} \end{equation}\]
  • step M: compute the mapping function \(\hat{\theta}_q:=M(\theta | \hat{\theta}_{q-1})=\arg \max Q(\theta| \hat{\theta}_{q-1})\) which maximises the auxiliary function. One way of retrieving the MLE associated to the auxiliary function is to determine the roots of its derivative, namely solving Equation (10)3:
\[\begin{equation} \frac{\partial Q(\theta| \hat{\theta}_{q-1})}{\partial \theta}=0 \tag{10} \end{equation}\]

Interestingly, the decomposition of the incomplete log-likelihood associated to a mixture model \(\ell(\theta|X)\) reveals an entropy term and the so-called auxiliary function (Dempster et al. 1977). It can be used to prove that maximising the auxiliary function at each step induces a bounded increase of the incomplete log-likelihood. Namely, the convergence of the EM algorithm, defined by comparisons of consecutive log-likelihood, is guaranteed, provided the mapping function returns the maximum of the auxiliary function. Yet, the convergence of the series of estimated parameters \((\theta_q)_{q \ge 0} \underset{i\to +\infty}{\longrightarrow} \hat{\theta}\) is harder to prove but has been formally demonstrated for the exponential family (a superset of the Gaussian family), as stated in Dempster et al. (1977).

Additionally, the EM algorithm is deterministic, meaning that for a given initial estimate \(\theta_0\) the parameters returned by the algorithm at a given step \(q\) are fixed. However, this method requires the user to provide an initial estimate, denoted as \(\theta_0\), of the model parameters and to specify the number of components in the mixture. We review some classic initialisation methods in Initialisation of the EM algorithm and some algorithms used to overcome the main limitations of the EM algorithm in the Appendix Extensions of the EM algorithm to overcome its limitations.

Finally, the prevalent choice of Gaussian distributions to characterize the distribution of random observations is guided by a set of interesting properties. In particular, Geary (1936) has shown that the Normal distribution is the only distribution for which the Cochran’s theorem (Cochran 1934) is guaranteed, namely for which the the mean and variance of the sample are independent of each other. Additionally, similar to any distribution proceeding from the exponential family, the MLE statistic is sufficient4.

1.4 Initialisation of the EM algorithm

EM-like algorithms require an initial estimate of the parameters, \(\theta_0\), to optimise the maximum likelihood. Initialisation is a crucial step, as a bad initialisation can possibly lead to a local sub-optimal solution or trap the algorithm in the boundary of the parameter space. The most straightforward initialisation methods, such as random initialisation, are standalone and do not require any additional initialisation algorithms, whereas meta-methods, such as short-EM, still need to be initialised by alternative methods. The commonly-used initialisation methods encompass:

The rebmix algorithm can thus be seen as a natural extension of the quantile method, with more rigorous statistical support. Two drawbacks of the algorithm include the need for intensive calibration of hyperparameters and its inadequacy for the estimation of highly overlapping or high dimensional mixture distributions6.

Following this theoretical introduction, we empirically evaluate the performance of the aforementioned R packages, considering various initialization algorithms and the complexity of the GMMs distributions. Precisely, we outline the simulation framework used to compare the seven packages in Methods and report the results in Results. We conclude by providing a general simplified framework to select the combination of package and initialisation method best suited to its objectives and the nature of the distribution of the dataset.

2 A comprehensive benchmark comparing estimation performance of GMMs

We searched CRAN and Bioconductor mirrors for packages that can retrieve parameters of GMM models. Briefly, out of 54 packages dealing with GMMs estimation, we focused on seven packages that all estimate the MLE in GMMs using the EM algorithm, were recently updated and allow the users to specify their own initial estimates: bgmm, EMCluster, flexmix, GMKMcharlie, mclust, mixtools and Rmixmod. The complete inclusion process is detailed in Appendix C, the meta-analysis workflow for the final selection of CRAN and Bioconductor platforms. The flowchart summarising our choices is represented in Figure 1.

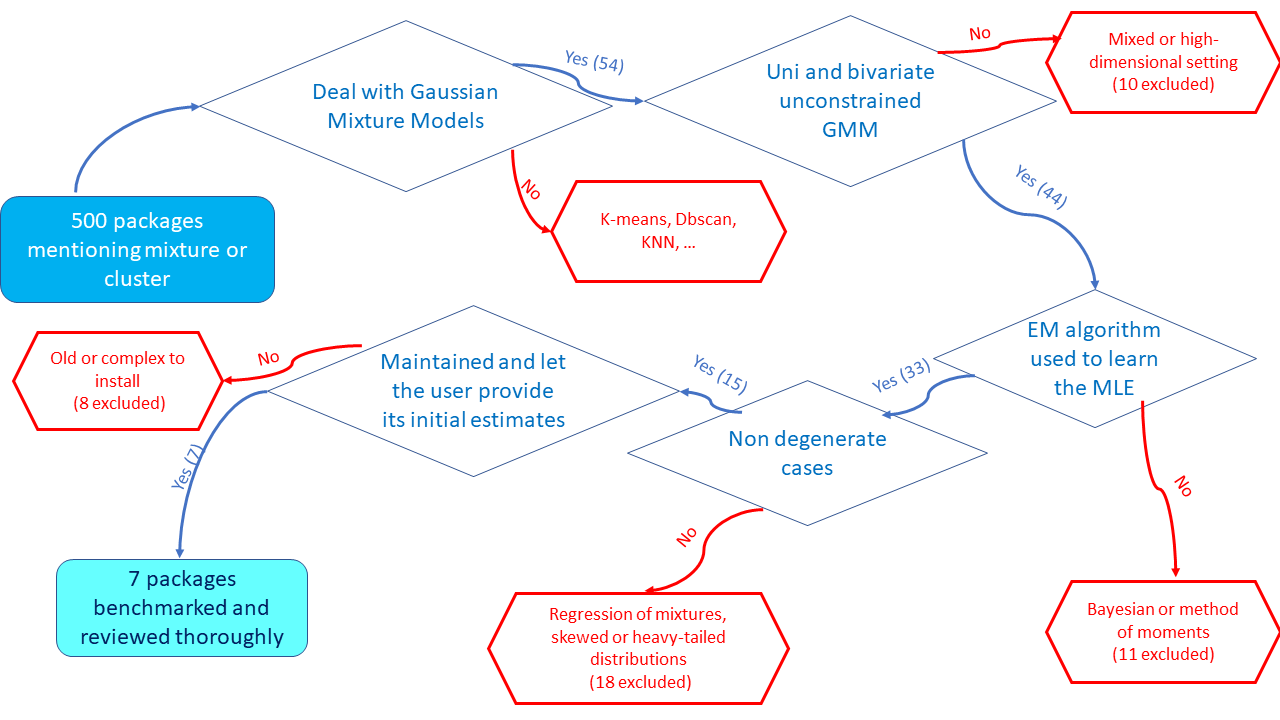
From root to top, we describe schematically the filtering process used for the final selection of the reviewed packages

Figure 1: A minimal roadmap used for the selection of the packages reviewed in our benchmark.

We also include two additional packages dedicated specifically to high-dimensional settings, namely EMMIXmfa (Rathnayake et al. 2019) and HDclassif (Berge et al. 2019) to compare their performance with standard multivariate approaches in complex, but non degenerate cases. We summarise the main features and use cases of the seven + two reviewed packages in Table 1. The three most commonly used packages are mixtools, mclust and flexmix. However, the mclust package is by far the most complete with many features provided to visualise and evaluate the quality of the GMM estimate. bgmm has the greatest number of dependencies, while mclust only depends of base R packages. Additionally, in parallel to clustering tasks, flexmix and mixtools packages perform regression of mixtures and implement mixture models using other parametric distributions or non-parametric methods via kernel-density estimation.

Table 1: Main features of the reviewed packages, sorted by decreasing number of daily downloads. Downloads per day returns the daily average number of downloads for each package on the last 2 years. Recursive dependencies column counts the complete set of non-base packages required, as first-order dependencies depend on other packages as well.

Package

Version

Regression

Implemented models

Downloads per day

Last update

Imports

Recursive dependencies

Language

mclust

5.4.7

5,223

31/10/2022

R (≥ 3.0)

0

Fortran

flexmix

2.3-17

Poisson, binary, non-parametric, semi-parametric

3,852

07/06/2022

R (≥ 2.15.0), modeltools, nnet, stats4

3

R

mixtools

1.2.0

multinomial, gamma, Weibull, non-parametric, semi-parametric

178

05/02/2022

R (≥ 3.5.0), kernlab, segmented, survival

6

C

Rmixmod

2.1.5

39

18/10/2022

R (≥ 2.12.0), Rcpp, RcppEigen

4

C++

EMCluster

0.2-13

33

12/08/2022

R (≥ 3.0.1), Matrix

3

C

bgmm

1.8.4

27

10/10/2021

R (≥ 2.0), mvtnorm, combinat

77

R

GMKMcharlie

1.1.1

12

29/05/2021

Rcpp, RcppParallel, RcppArmadillo

3

C++

EMMIXmfa

2.0.11

12

16/12/2019

0

C

HDclassif

2.2.0

35

12/10/2022

rARPACK

13

R

We further detail features specifically related to GMMs in Table 2. We detail row after row its content below:

High-dimensional packages provide specific representations adjusted to the high-dimensional settings, notably allowing the user to visualise the projected factorial representation of its dataset in a two or three-dimensional subspace. They also provide specialised performance plots, notably scree plots or BIC scatter plots to represent in a compact way numerous projections and parametrisations.

Table 2: Custom features associated to GMMs estimation for any of the benchmarked packages.

Package features

mclust

flexmix

mixtools

Rmixmod

EMCluster

bgmm

GMKMcharlie

EMMIXmfa

HDclassif

Models Available (univariate)

canonical

unconstrained

canonical

canonical

unconstrained

canonical

unconstrained

Models Available (multivariate)

canonical

unconstrained diagonal or general

unconstrained

canonical

unconstrained

4 models (diagonal and general, either component specific or global)

unconstrained

4 models (either component-wise or common, on the intrinsic and diagonal residual error covariance matrices)

canonical on projected dimension

Variants of the EM algorithm

VBEM

SEM, CEM

ECM

SEM, CEM

CW-EM, MML

AECM

SEM, CEM

Initialisation

hierarchical clustering, quantile

short-EM, random

random

random, short-EM, CEM, SEM

random, short-EM

k-means, quantile

k-means

k-means, random, heuristic

short-EM, random, k-means

Model or Cluster Selection

BIC, ICL, LRTS

AIC, BIC, ICL

AIC, BIC, ICL, CAIC, LRTS

BIC, ICL, NEC

AIC, BIC, ICL, CLC

GIC

BIC, ICL, CV

Bootstrap Confidence Intervals

Visualisation

performance, histograms and boxplots of bootstrapped estimates, density plots (univariate), scatter plots with uncertainity regions and boundaries (bivariate), isodensity (bivariate , 2D projected PCA or selecting coordinates)

density curves

density curves, scatter plots with uncertainty boundaries

performance, scatter plots with uncertainty boundaries

projected factorial map

projected factorial map, performance (Cattell's scree plot, BIC performance, slope heuristic)

2.1 Methods

In addition to the the seven packages selected for our benchmark, we include a custom R implementation of the EM algorithm used as baseline, referred to as RGMMBench, and for the high-dimensional setting we select packages EMMIXmfa and HDclassif, on the basis of criteria detailed in Appendix C, General workflow. Code for RGMMBench is provided in Appendix Application of the EM algorithm to GMMs. To compare the statistical performances of these packages, we performed parametric bootstrap (Derivation of confidence intervals in GMMs) and built an experimental design to cover distinct mixture distributions parameter configurations, using prior user-defined parameters.

For each experiment, we assign each observation to an unique cluster by drawing \(n\) labels \(S_{1:n}\) from a multinomial distribution whose parameters were the prior user-defined proportions \(p=(p_1, \ldots, p_k)\). Then, each observation \(x_i\) assigned to hidden component \(j\) is drawn from a Normal distribution using the stats::rnorm() function for the univariate distribution and MASS::mvrnorm for the multivariate distribution. The complete code used for simulating data is available on GitHub at RGMMBench. Finally, we obtain an empirical distribution of the estimated parameters by computing the MLE of each randomly generated sample.

For all the packages, we used the same convergence threshold, \(10^{-6}\), and maximum of 1,000 iterations, as a numerical criterion for convergence. We generated simulated data with \(n = 200\) observations in the univariate setting and \(n = 500\) observations in the bivariate setting. We set the number of observations in order to minimise the probability of generating a sample without drawing any observations from one of the components7. Unless stated explicitly, we kept the default hyper-parameters and custom global options provided by each package. For instance, the flexmix package has a default option, minprior, set by default to 0.05, which removes any component present in the mixture with a ratio below \(0.05\). Besides, the fully unconstrained model was the only one which we implemented both in the univariate and multivariate settings, as it is the only parametrisation implemented in all the seven packages.

We compared the packages’ performances using five initialisation methods: random, quantile, k-means, rebmix and hierarchical clustering in the univariate setting. We benchmarked the same initialisation methods in the multivariate setting, except for the quantile method which has no multivariate equivalent (see section Initialisation of the EM algorithm):

We sum up in Table 3 the general configuration used to run the scripts. Additionally, all simulations were run with the same R (R Core Team 2023) version 4.0.2 (2020-06-22).

Table 3: Global options shared by all the benchmarked packages.

Initialisation methods

Algorithms

Criterion threshold

Maximal iterations

Number of observations

hc, kmeans, small EM,rebmix, quantiles, random

EM R, Rmixmod, bgmm, mclust, flexmix, EMCluster, mixtools, GMKMCharlie

10−610^{-6}

1,000

100, 200, 500, 1000, 2000, 5000, 10000

Preliminary experiments suggested that the quality of the estimation of a GMM is mostly affected by the overlap between components’ distribution and level of unbalance between components. We quantified the overlap between two components by the following overlap score (OVL, see Equation (11)), with a smaller score denoting well-separated components:

\[\begin{equation} \operatorname{OVL}(i, j) = \int \min (f_{\zeta_i} (x), f_{\zeta_j} (x)) dx \quad \text{ with } i \neq j \tag{11} \end{equation}\]

We may generalise this definition to \(k\) components by averaging the individual components’ overlap. We use the function MixSim::overlap from the MixSim package (Melnykov et al. 2021) that approximates this quantity using a Monte-Carlo based method (see appendices An analytic formula of the overlap for univariate Gaussian mixtures and Practical details for the implementation of our benchmark for further details).

The level of imbalance may be evaluated with entropy measure (Equation (12)):

\[\begin{equation} H(S)=-\sum_{j=1}^k p_j \log_k (p_j) \tag{12} \end{equation}\]

with \(k\) is the number of components and \(p_j=\mathbb{P}(S=j)\) is the frequency of class \(j\).

We considered 9 distinct configuration parameters, associated with distinct values of \(\operatorname{OVL}\) and entropy in the univariate setting, 20 configurations in the bivariate setting, and 16 configurations in the high-dimensional setting. Briefly, in the univariate setting, we simulated components with the same set of four means (0, 4, 8, and 12), three sets of mixture proportions
\(\left[(0.25, 0.25, 0.25, 0.25); (0.2, 0.4, 0.2, 0.2); (0.1, 0.7, 0.1, 0.1) \right]\) and three variances: \((0.3, 1, 2)\). In the bivariate setting, we consider two sets of proportions: \(\left[(0.5, 0.5); (0.9, 0.1) \right]\), two sets of coordinate centroids: \(\left[(0; 20), (20, 0) \right]\) and \(\left[(0; 2), (2, 0) \right]\), the same variance of 1 for each feature and for each component for illustrative purposes of the direct relation linking the correlation and the level of OVL and five sets of correlation:\([(-0.8, -0.8); (0.8, -0.8); (-0.8, 0.8); (0.8, 0.8); (0, 0)]\).

Finally, we tested eight configurations in the high-dimensional framework, setting to \(D=10\) the number of dimensions. We modified the level of overlap (definition is reported in Equation (11)) and the imbalance between the component proportions across our simulations. Additionally, we tested two types of constraints on the covariance matrix: fully parametrised and spherical (see Appendix Parsimonious parametrisation of multivariate GMMs). Each of the parameter configurations tested in the high-dimensional setting was evaluated with \(n=200\) observations and \(n=2000\) observations. Additionally, instead of manually defining the parameters for the high-dimensional simulation, we used the MixSim::MixSim function from the MixSim package (Melnykov et al. 2021). This function returns the user a fully parametrised GMM, with a prior defined level of maximum or average overlap8.

The complete list of parameters used is reported respectively in Table 4 for the univariate setting, Table 5 for the bivariate setting and 6 for the high-dimensional setting. We benchmarked simulations where the components were alternatively very distinct or instead very overlapping, as well as of equal proportions or instead very unbalanced. The adjustments made to meet the specific requirements of high dimensional packages are detailed in Practical details for the implementation of our benchmark.

We report the most significant results and features and the associated recommendations in next section Results.

2.2 Results

All figures and performance overview tables are reported in Supplementary Figures and Tables in the univariate simulation for the univariate setting, Supplementary Figures and Tables in the bivariate simulation for the bivariate scenario and Supplementary Figures and Tables in the HD simulation for the high dimensional scenario.

Balanced and non-overlapping components

In the univariate setting, with balanced components and low \(\operatorname{OVL}\) (scenario U1 in Table 4), the parameter estimates are identical in most cases across initialisation methods and packages, notably the same estimates are returned with k-means or rebmix initialisation. However, the random initialisation method leads to a higher variance and bias on the parameter estimates than other methods (Supplementary Figure 4 and Supplementary Table 6), with some estimates fitting only local maxima, far from the optimal value.

Similarly, the scenarios in the bivariate setting (configurations B6-B10 in Table 5), with a focus on B6, B7 and B10 visualised in Supplementary Figure 16, feature well-separated and balanced components. Consistent with conclusions from the corresponding univariate configurations, all benchmarked packages return the same estimates across initialisation methods.

Unbalanced and non-overlapping components

However, with unbalanced classes and low \(\operatorname{OVL}\) (scenario U7 in 4), the choice of the initialisation method is crucial, with quantiles and random methods yielding more biased estimates and proned to fall in local maximum. Rebmix initialisation provides the best estimates, with the smallest MSE and bias across packages (Supplementary Figure 5 and supplementary Table 7, always associated with the highest likelihood. Overall, with well-discriminated components, most of the differences on the estimation originate from the choice of initialisation method, while the choice of the package has only small impact.

In the bivariate framework, two configurations featured both strongly unbalanced and well-separated components, similarly to scenario U3 in Table 4: the configurations B12 (Supplementary Figure 12 and Table 12) and B14 (Supplementary Figure 13 and Supplementary Table 13). Similarly, configurations B16, B17 and B20 (Table 5) with similar characteristics are summarised in supplementary Figure 17. In all these configurations, neither the initialisation method nor the package have a statistical significant impact on the overall performance.

Similarly, configurations HD1a-HD4b in Table 6) in the high dimensional setting display well-separated clusters, with a representative outcome represented in Supplementary Figure 19 and Supplementary Table 16. Consistent with the results obtained in the analogous univariate and bivariate scenarios, in the unbalanced and non-overlapping framework, the majority of the benchmarked packages produce highly consistent and similar estimates when hierarchical clustering and k-means were used for parameter initialisation. However, bgmm and EMCluster clearly perform worse when the rebmix initialization method is used (however, overall, rebmix performs poorly, regardless of the package used for estimation). Notably, initialisations with the rebmix package tend to display a much larger number of poor estimations, some of which can be identified with the local maxima associated with parameter switching between the two classes. Finally, the two additional packages dedicated to high-dimensional clustering display the worst performances, with EMMIXmfa returning the most biased parameters and HDclassif the most noisy estimates. EMMIXmfa is the only package that returned highly biased estimates of the components’ proportions in this setting.

Balanced and overlapping components

When the overlap between components increases, the bias and variability of the estimates tends to increase, and the choice of initialisation method becomes more impactful. The least biased and noisy estimations with balanced components in the univariate setting (scenario U3 in Table 4) are obtained with the k-means initialisation (Supplementary Figure 3 and Table 8) while the rebmix initialisation returns the most biased and noisy estimates. Similar results are found in the bivariate setting with a balanced and highly overlapping two-component GMM (configurations B1-B5 from Table 5), with the best performance reached with the k-means initialisation method, followed by MBHC. This is emphasised in supplementary Figure 16, in the top three most complex configurations, namely B1, B2 and B5. If the shape of the covariance matrix is well-recovered, no matter the package, the Hellinger distances are significantly higher (and thus the estimate further away from the target distribution) with the random and rebmix methods.

Similarly, in the high-dimensional scenario HD7 of Table 6), presenting balanced but highly overlapping clusters with a full covariance structure, the best performance was obtained with k-means initialisation, while the rebmix initialisation returned the most biased and noisy estimates. While EMMIXmfa performed well when it converged, it returned an error in most cases (see Column Success of supplementary Table 17). The least biased estimates were returned by mixtools and Rmixmod and the least noisy by flexmix, mclust and GMKMCharlie (smaller MSE). Interestingly, in the high-dimensional setting, the packages EMCluster and bgmm exhibited worse performance. In particular, as can be seen in panel E of supplementary Figure 20, the proportions of the components recovered the \(]0-1[^k\) simplex.

Conversely, the EMCluster package, and to a lesser extent, the bgmm package, performed surprisingly well when datasets were simulated with an underlying spherical covariance structure, even though the estimation was not performed explicitly with this constraint (Supplementary Table 19). Indeed, it seems like that the off-diagonal terms tended to converge towards 0, as showcased in Supplementary Figure 21, in Panel C, in which the fourth row from top represents the bootstrap intervals associated to the pairwise covariance between dimension 1 and 2 of each cluster.

Unbalanced and overlapping components

With unbalanced components and high \(\operatorname{OVL}\) (scenario U9 in Table 4), all packages, no matter the initialisation method, provided biased estimates, with a higher variability of the parameter estimates compared to other configurations. The least biased estimates were obtained with k-means or random initialisation, but with a higher variability on the estimates with random initialisation (Supplementary Table 9). Delving further into the individual analysis of the parameter estimates associated to each component, we found out that the least biased estimates were achieved with rebmix initialisation for the most distinguishable components. For instance, in our configuration, the clusters 2 and 4 (see Supplementary Figure 7 and Table 9) were better characterised with the rebmix method. This observation aligns with the rebmix’s underlying framework, using the modes of the distribution for initialising the component (Nagode 2015). With highly-overlapping distributions and unbalanced components, both the choice of the initialisation algorithm and the package have a substantial impact on the quality of the estimation of this mixture.

Two configurations in our bivariate simulation feature distributions with both strong OVL and unbalanced components. Especially, the scenario B11 (Table 5) has the strongest OVL overall, with notably a risk of wrongly assigning minor component 2 to major component 1 of 0.5 (a random method classifying each observation to cluster 1 or 2 would have the same performance).

First, we observe that the the random and rebmix initialisation methods have similar performance, significantly better than \(k\)-means or MBHC (Supplementary Figure 11). Specifically, the rebmix method returns the least biased estimates, while the random method is associated with the lowest MSE (respectively for configurations B11 and B15, the supplementary Tables 11 and 14). Second, the estimates differ across packages only in these two complex configurations, with packages Rmixmod and mixtools returning more accurate estimates than the others. It it is particularly emphasised in Scenario B15, where the component-specific covariance matrices are diagonal with same non-null input, and thus should present spherical density distributions. However, only the first class of packages correctly recovers the spherical bivariate \(95\%\) confidence regions while they are slightly ellipsoidal with the second class of packages (Panel B, Supplementary Figure 14).

With full covariance structures and unbalanced proportions, as depicted in the high-dimensional Scenario HD8a) and b) of Table 6, the general observations stated in the previous subsection for the high dimensional setting hold, namely that the least biased estimates are returned by packages not specifically designed for high-dimensional data, with the k-means initialisation (Supplementary Table 12 and supplementary Figure 22). Furthermore, the EMCluster and bgmm packages and the two packages dedicated to high-dimensional, perform similarly with \(n=200\) observations (sub-scenario a) and \(n=2000\) observations (sub-scenario b), whereas we would expect narrower and less biased confidence intervals by increasing the number of observations by a factor of 10.

Finally, with spherical covariance structures and unbalanced proportions, the best performances, both in terms of bias and variability, are obtained with flexmix, mclust and GMKMCharlie. Indeed, as detailed later in Conclusions, these packages are more sensitive to the choice of the initialisation method and have a greater tendency to get trapped in the neighbourhood of the initial estimates (Supplementary Table 19 and supplementary Figure 22). Accordingly, k-means initialisation performs best since it assumes independent and homoscedastic features for each cluster. Furthermore, EMMIXmfa is the package that best estimates the off-diagonal terms in this setting, as highlighted in supplementary Table 19.

Identification of two classes of packages with distinct behaviours

By summarizing the results obtained across all simulations, we identify two classes of packages with distinct behaviours (Figure 2):

Panels A, B and C display, respectively in the univariate, bivariate and high-dimensional setting, the heatmap of the Pearson correlation between the estimated parameters across the benchmarked packages for the most discriminative scenario (the one featuring the most unbalanced and overlapping components): scenario U9, Table 4 in the univariate setting, scenario B11, Table 5, for the bivariate simulation and scenario HD8, Table 6 for the high-dimensional simulation, with the k-means initialisation.

We further identified with this representation minor differences for the estimation of the parameters between Rmixmod and mixtools, while three subgroups can be identified in the second class of packages: the first subset with bgmm and mclust, the second subset with EMCluster and GMKMcharlie packages and the flexmix package, which clearly stands out from the others, as being the one most likely to be trapped at the boundaries of the parameter space. After examining the source codes of the packages, we attribute this differences to custom implementation choices of the EM algorithm, such as the way numerical underflow is managed or the choice of a relative or absolute scale to compare consecutive computed log-likelihoods (see Appendix EM-implementation differences across reviewed packages and Panel D, Figure 2). In the high-dimensional setting, the second class of packages showed additional heterogeneity, with EMCluster and bgmm setting themselves apart from the other three packages.

Panels A, B and C show respectively the heatmap of the Pearson correlation in the univariate, bivariate and high-dimensional framework between the parameters estimated by the packages, evaluated for the most discriminating and complex scenario. The correlation matrix was computed using the function <a href='https://rdrr.io/r/stats/cor.html'>stats::cor</a> with option *complete* to remove any missing value related to a failed simulation, and the heatmap generated with the Bioconductor package *ComplexHeatmap*. Panel D represents a tree summarising the main differences between the benchmarked packages, in terms of the EM implementation. They are discussed in more detail in Appendix *EM-implementation differences across reviewed packages*.

Figure 2: Panels A, B and C show respectively the heatmap of the Pearson correlation in the univariate, bivariate and high-dimensional framework between the parameters estimated by the packages, evaluated for the most discriminating and complex scenario. The correlation matrix was computed using the function stats::cor with option complete to remove any missing value related to a failed simulation, and the heatmap generated with the Bioconductor package ComplexHeatmap. Panel D represents a tree summarising the main differences between the benchmarked packages, in terms of the EM implementation. They are discussed in more detail in Appendix EM-implementation differences across reviewed packages.

Failed estimations

Finally, in some cases, neither the specific EM algorithm implemented by each package nor the initialisation method were able to return an estimate with the expected number of components, or converged to a degenerate distribution (e.g., with infinite or zero variances). In that case, we considered the estimation as failed and accordingly we did not include it into the visualisations and the summary metric tables.

Most of the failed estimations occurred with the rebmix initialisation. Indeed, an updated version of the package forced the user to provide a set of possible positive integer values for the number of components, with at least a difference of two between the model with the most components and the model with the least components (we therefore set the parameter cmax to \(k+1\) and cmin to \(k-1\)).In scenarios where the distributions associated with each cluster exhibit significant overlap, there is an increased risk of incorrectly estimating the number of components. This arises from the inherent difficulty of discerning the modes within the overall distribution. For instance, in the most complex scenario B11, characterized by strong overlap and imbalanced clusters (refer to Table \(\ref{tab:parameter-configuration-bivariate}\)), up to \(20\%\) of initialisations were unsuccessful. Similarly, in the second most challenging scenario, B15, approximately \(10\%\) of initializations failed against an averaged number of \(4\%\) of the simulations exhibiting an inaccurate estimation of the number of components.

Removing errors proceeding from the initialisation method, only the flexmix package failed in returning an estimate matching the user criteria in some configurations of the univariate and bivariate settings. In both cases, the strong assumption that any cluster with less than \(5\%\) of the observations is irrelevant, results in trimming one or more components9. This strong agnostic constraint on component proportions led to failures in configurations featuring strongly overlapping clusters, with up to \(20\%\) failed estimations with the random initialisation method in scenario B11 (Table 5) and \(80\%\) failed estimations in the univariate setting10 with the rebmix initialisation with scenario U9, Table 4.

In a relatively high dimensional framework, as tested on our third benchmark (Table 6), none of the algorithms that were initialised with the random method (EMCluster::rand.EM()) converged successfully. Indeed, of the 16 configurations tested, the covariance returned during the initialisation was systematically non-positive definite for at least one of the components, violating the properties of covariance matrices. Furthermore, an analysis of summary metrics in scenarios HD1 and HD8, reported in supplementary Tables 20 and 21, revealed a notably higher rate of failures when employing rebmix initialisation in conjunction with packages tailored for high dimensionality, such as HDclassif EMMIXmfa. This discrepancy was in stark contrast to the more reliable and consistent initial estimates returned by \(k\)-means or hierarchical clustering.

Furthermore, as shown by the comparison of summary metrics with \(n=200\) and \(n=2000\) observations in supplementary Tables 20 and 21, respectively for the simplest scenario HD1 and the most complex one HD8, the rebmix initialisation on the one hand, and the packages dedicated to high dimensionality or those of the second class of packages that show a particular behaviour, present much more failures than the k-means or hierarchical clustering initialisation.

3 Conclusions

There are many packages that implement the EM algorithm for estimating the parameters of GMMs. But only few are regularly updated, implement both the unconstrained univariate and multivariate GMM, and enable the user to provide its own initial estimates. Hence, among the 54 packages dealing with GMMs available on CRAN or Bioconductor repositories, we focused our review on 7 packages which implement all of these features. We believe that our in-depth review of the packages can help users to quickly find the best package for their clustering pipeline and highlight limitations in the implementation of some packages. Our benchmark covers a much broader range of configurations than the previously-published studies (Leytham 1984; Nityasuddhi and Böhning 2003; Xu and Knight 2010; Lourens et al. 2013), as we studied the impact of the level of overlap and the imbalance of the mixture proportions on the quality of the estimation.

Interestingly, the EM algorithm occasionally yields biased and inefficient estimates when the components overlap a lot, which agrees with the past literature (Leytham 1984; Xu and Knight 2010; Lourens et al. 2013). This appears to go counter to the theoretical results presented by Leytham (1984), which demonstrated the asymptotic consistency, unbiasedness, and efficiency of maximum likelihood estimates of GMMs. However, it’s important to note that this theoretical demonstration relies on the definition of a “local” environment, necessitating the prior setting of boundaries within which the theorem’s conditions are met (in other words, the definition of the support, which delineates the region where the initial values can be sampled from). It’s not then surprising that the EM algorithm struggles in reaching the global maximum of the distribution in the presence of multiple local extremes.

When all components are well-separated or have a relatively small number of components (three or fewer), we found that the best estimation (lowest MSE and bias) is reached with the latest initialisation method developed, namely the rebmix one. Notably, the global maximum is always properly found in our simulations with distinguishable components. Yet, with overlapping components, the least biased and variable estimates overall are obtained with k-means initialisation, enforcing the robustness of the method while the assumptions for using it are not met.

On the contrary, with unbalanced and numerous components (above three), the quantiles initialisation leads to the most biased estimates while the rebmix initialisation induces the highest variability. Indeed, rebmix initialisation is not fit for highly overlapping mixtures, since one of its most restrictive assumption is that each generated interval of the empirical mixture distribution can be associated unambiguously to a component (see Initialisation of the EM algorithm and Nagode (2015)).

Furthermore, rebmix is not particularly adjusted to deal with high-dimensional mixtures, displaying systematically poorer performance compared to other initialisation strategies, such as k-means or hierarchical clustering, as illustrated by the summary metrics listed in Appendix Supplementary Figures and Tables in the HD simulation. Higher risk of returning a sub-optimal extremum likely arises from the increased data sparsity in high dimensional datasets, which grows as the square root of the number of dimensions \(\sqrt{D}\) (Convergence of distance definitions). Thus, we expect that most of the equally-large intervals binning the sampling space and that are used to initiate the rebmix algorithm contain either no or only observation, preventing from retrieving the numerically defined mode of the distribution and increasing the risk of initiating the algorithm in a spurious neighbourhood.

About the remaining initialisation strategies, we observed that, even in the well-separated case, random initializations can sometimes yield highly biased estimates, far from the true parameter values. Consistent with our observations, it was shown in Jin et al. (2016) that the probability for the EM algorithm to converge from randomly initialised estimates to a local suboptimal maximum is non null above two components, increasing with the number of components. Additionally, the local maximum of the likelihood function obtained can be arbitrarily worse than the global maximum. Finally, hierarchical clustering does not take into account any uncertainty on the assignment for an observation to a given class, which explains its rather bad performances with overlapping components. Overall, there is always an initialisation algorithm performing better than the hierarchical clustering, and further it is also by far the slowest and most computationally intensive initialisation method (see supplementary Figure 10).

Our study reveals that while the EM algorithm is supposed to be deterministic, the estimates obtained from its implementations can differ across packages. We were able to link these differences with custom choices of EM implementations across the benchmarked packages. Two distinct classes of packages emerge, each with specific approaches to address certain limitations of the EM algorithm. The first class, exemplified by mixtools and Rmixmod typically yields smaller but less biased estimates that exhibit lower sensitivity to the choice of initialization method. However, these estimates tend to have higher variability and require longer running times to achieve convergence. The second class, composed of the remaining packages, provide estimates with reduced MSE, but at the extent of a higher bias on the estimates. One plausible explanation is that the first class of packages, comparing absolute iterations of the function to be maximised, tends on average to perform more iterations. The estimated results are accordingly more consistent and closer to the true MLE estimation but at the expense of an increased risk of getting trapped in a local extrema or a plateau, explaining the greater number of outliers observed. Among them, flexmix stands out by choosing an unbiased but non MLE-estimate of the covariance matrix, without any clear improvement of the overall performance in our simulations.

Based on these results, we design a decision tree indicating the best choice of package and initialisation method in relation with the shape of the distribution, displayed in Figure 3. Interestingly, our conclusions are consistent between the univariate and bivariate settings. Furthermore, most of the general recommendations on the best choices of packages with respect to the characteristics of the mixture model generally hold in a relatively higher dimensional setting11. From this, we assume that projection into a lower-dimensional space is only beneficial in a very high-dimensional setting, for example when the number of dimensions exceeds the number of observations, or when unrestricted parameter estimation (with the full covariance structure) is practically infeasible for computational reasons.

A decision tree to select the best combination of package and initialisation method with respect to the main characteristics of the mixture. It's worth pointing that in both univariate and low dimension multivariate settings, the recommandations are similar.

Figure 3: A decision tree to select the best combination of package and initialisation method with respect to the main characteristics of the mixture. It’s worth pointing that in both univariate and low dimension multivariate settings, the recommandations are similar.

Comparing all these packages suggest several improvements.

  1. The use of C++ code speeds up the convergence of the EM algorithm compared to a native R implementation.

  2. All packages dealing with GMMs should use k-means for overlapping, complex mixtures and rebmix initialisation for well-separated components, provided that the dimension of the dataset is relatively small. The final choice between these two could be set after a first run or visual inspection aiming at determining roughly the level of entropy across mixture proportions and the degree of overlap between components.

  3. The packages should allow the user to set their own termination criteria (either relative or absolute log-likelihood or over the estimates after normalisation). Interestingly, EMMIXmfa is the only package among those examined that allows the user to consider an absolute or relative convergence endpoint of the EM algorithm, through the conv_measure attribute, with diff and ratio options respectively.

  4. With a great number of components or complex overlapping distributions, the optimal package should integrate prior information when available, e.g. via Bayesian estimation.

While mclust appeared as the most complete package to model GMMs in R, none of the packages reviewed in this report features all the characteristics mentioned above. We thus strongly believe that our observations will help users identify the most suitable packages and parameters for their analyses and guide the development or updates of future packages.

4 Simulation settings

For ease of reading, we reproduce below the parameter configurations used to run the three benchmarks, respectively for the univariate (Table 4), bivariate (5) and high dimensional setting (Table 6).

Table 4: The 9 parameter configurations tested to generate the samples of the univariate experiment, with \(k=4\) components.
ID Entropy OVL Proportions Means Correlations
U1 1.00 3.3e-05 0.25 / 0.25 / 0.25 / 0.25 0 / 4 / 8 / 12 0.3 / 0.3 / 0.3 / 0.3
U2 1.00 5.7e-03 0.25 / 0.25 / 0.25 / 0.25 0 / 4 / 8 / 12 1 / 1 / 1 / 1
U3 1.00 2.0e-02 0.25 / 0.25 / 0.25 / 0.25 0 / 4 / 8 / 12 2 / 2 / 2 / 2
U4 0.96 3.3e-05 0.2 / 0.4 / 0.2 / 0.2 0 / 4 / 8 / 12 0.3 / 0.3 / 0.3 / 0.3
U5 0.96 5.8e-03 0.2 / 0.4 / 0.2 / 0.2 0 / 4 / 8 / 12 1 / 1 / 1 / 1
U6 0.96 2.0e-02 0.2 / 0.4 / 0.2 / 0.2 0 / 4 / 8 / 12 2 / 2 / 2 / 2
U7 0.68 2.7e-05 0.1 / 0.7 / 0.1 / 0.1 0 / 4 / 8 / 12 0.3 / 0.3 / 0.3 / 0.3
U8 0.68 4.4e-03 0.1 / 0.7 / 0.1 / 0.1 0 / 4 / 8 / 12 1 / 1 / 1 / 1
U9 0.68 1.5e-02 0.1 / 0.7 / 0.1 / 0.1 0 / 4 / 8 / 12 2 / 2 / 2 / 2
Table 5: The 20 parameter configurations tested to generate the samples of the bivariate experiment.
ID Entropy OVL Proportions Means Correlations
B1 1.00 0.15000 0.5 / 0.5 (0,2);(2,0) -0.8 / -0.8
B2 1.00 0.07300 0.5 / 0.5 (0,2);(2,0) -0.8 / 0.8
B3 1.00 0.07300 0.5 / 0.5 (0,2);(2,0) 0.8 / -0.8
B4 1.00 0.00078 0.5 / 0.5 (0,2);(2,0) 0.8 / 0.8
B5 1.00 0.07900 0.5 / 0.5 (0,2);(2,0) 0 / 0
B6 1.00 0.00000 0.5 / 0.5 (0,20);(20,0) -0.8 / -0.8
B7 1.00 0.00000 0.5 / 0.5 (0,20);(20,0) -0.8 / 0.8
B8 1.00 0.00000 0.5 / 0.5 (0,20);(20,0) 0.8 / -0.8
B9 1.00 0.00000 0.5 / 0.5 (0,20);(20,0) 0.8 / 0.8
B10 1.00 0.00000 0.5 / 0.5 (0,20);(20,0) 0 / 0
B11 0.47 0.06600 0.9 / 0.1 (0,2);(2,0) -0.8 / -0.8
B12 0.47 0.01600 0.9 / 0.1 (0,2);(2,0) -0.8 / 0.8
B13 0.47 0.05000 0.9 / 0.1 (0,2);(2,0) 0.8 / -0.8
B14 0.47 0.00045 0.9 / 0.1 (0,2);(2,0) 0.8 / 0.8
B15 0.47 0.03900 0.9 / 0.1 (0,2);(2,0) 0 / 0
B16 0.47 0.00000 0.9 / 0.1 (0,20);(20,0) -0.8 / -0.8
B17 0.47 0.00000 0.9 / 0.1 (0,20);(20,0) -0.8 / 0.8
B18 0.47 0.00000 0.9 / 0.1 (0,20);(20,0) 0.8 / -0.8
B19 0.47 0.00000 0.9 / 0.1 (0,20);(20,0) 0.8 / 0.8
B20 0.47 0.00000 0.9 / 0.1 (0,20);(20,0) 0 / 0
Table 6: The 16 parameter configurations tested to generate the samples in a high dimensional context. The first digit of each ID index refers to an unique parameter configuration (identified by its level of overlap, entropy and topological structure, either circular or ellipsoidal, of the covariance matrix, while the lowercase letter depicts the number of observations, a) with \(n=200\) and b) with \(n=2000\).
ID OVL Proportions Spherical
HD1a 1e-04 200 0.5 / 0.5
HD1b 1e-04 2000 0.5 / 0.5
HD2a 1e-04 200 0.19 / 0.81
HD2b 1e-04 2000 0.19 / 0.81
HD3a 1e-04 200 0.5 / 0.5
HD3b 1e-04 2000 0.5 / 0.5
HD4a 1e-04 200 0.21 / 0.79
HD4b 1e-04 2000 0.21 / 0.79
HD5a 2e-01 200 0.5 / 0.5
HD5b 2e-01 2000 0.5 / 0.5
HD6a 2e-01 200 0.15 / 0.85
HD6b 2e-01 2000 0.15 / 0.85
HD7a 2e-01 200 0.5 / 0.5
HD7b 2e-01 2000 0.5 / 0.5
HD8a 2e-01 200 0.69 / 0.31
HD8b 2e-01 2000 0.69 / 0.31

5 Additional files

5.1 Supplementary materials

Supplementary materials are available in addition to this article. It can be downloaded at RJ-2023-043.zip

J. Baek, G. J. McLachlan and L. K. Flack. Mixtures of Factor Analyzers with Common Factor Loadings: Applications to the Clustering and Visualization of High-Dimensional Data. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010. DOI 10.1109/TPAMI.2009.149.
J. D. Banfield and A. E. Raftery. Model-Based Gaussian and Non-Gaussian Clustering. Biometrics, 1993. DOI 10.2307/2532201.
L. Berge, C. Bouveyron and S. Girard. HDclassif: High dimensional supervised classification and clustering. 2019.
C. Biernacki, G. Celeux and G. Govaert. Choosing starting values for the EM algorithm for getting the highest likelihood in multivariate Gaussian mixture models. Computational Statistics & Data Analysis, 2003. DOI 10.1016/S0167-9473(02)00163-9.
C. Bouveyron and S. Girard. Robust Supervised Classification with Mixture Models: Learning from Data with Uncertain Labels. Pattern Recognition, 2009. DOI 10.1016/j.patcog.2009.03.027.
G. Celeux and G. Govaert. A classification EM algorithm for clustering and two stochastic versions. Computational Statistics & Data Analysis, 1992. DOI 10.1016/0167-9473(92)90042-E.
J. Chen. Consistency of the MLE under mixture models. 2016. DOI 10.1214/16-STS578.
W. G. Cochran. The distribution of quadratic forms in a normal system, with applications to the analysis of covariance. Mathematical Proceedings of the Cambridge Philosophical Society, 1934. DOI 10.1017/S0305004100016595.
A. P. Dempster, N. M. Laird and D. B. Rubin. Maximum Likelihood from Incomplete Data Via the EM Algorithm. Journal of the Royal Statistical Society, 1977. DOI 10.1111/j.2517-6161.1977.tb01600.x.
C. Fraley. Algorithms for Model-Based Gaussian Hierarchical Clustering. SIAM Journal on Scientific Computing, 1998. DOI 10.1137/S1064827596311451.
R. C. Geary. The Distribution of "Student’s" Ratio for Non-Normal Samples. Supplement to the Journal of the Royal Statistical Society, 1936. DOI 10.2307/2983669.
C. Jin, Y. Zhang, S. Balakrishnan, et al. Local Maxima in the Likelihood of Gaussian Mixture Models: Structural Results and Algorithmic Consequences. 2016. DOI https://doi.org/10.48550/arXiv.1609.00978.
B. O. Koopman. On Distributions Admitting a Sufficient Statistic. Transactions of the American Mathematical Society, 1936. DOI 10.2307/1989758.
W. Kwedlo. A New Method for Random Initialization of the EM Algorithm for Multivariate Gaussian Mixture Learning. In Proceedings of the 8th International Conference on Computer Recognition Systems CORES 2013, Eds R. Burduk, K. Jackowski, M. Kurzynski, M. Wozniak and A. Zolnierek 2013. Springer International Publishing. ISBN 978-3-319-00969-8. DOI 10.1007/978-3-319-00969-8\_8.
K. M. Leytham. Maximum Likelihood Estimates for the Parameters of Mixture Distributions. Water Resources Research, 1984. DOI 10.1029/WR020i007p00896.
S. Lourens, Y. Zhang, J. D. Long, et al. Bias in Estimation of a Mixture of Normal Distributions. Journal of biometrics & biostatistics, 2013. DOI 10.4172/2155-6180.1000179.
G. McLachlan and D. Peel. Finite Mixture Models: McLachlan/Finite Mixture Models. John Wiley & Sons, Inc., 2000. DOI 10.1002/0471721182.
V. Melnykov, W.-C. Chen and R. Maitra. MixSim: Simulating data to study performance of clustering algorithms. 2021.
M. Nagode. Finite mixture modeling via REBMIX. Journal of Algorithms and Optimization, 2015.
M. Nagode. Rebmix: Finite mixture modeling, clustering & classification. 2022.
D. Nityasuddhi and D. Böhning. Asymptotic properties of the EM algorithm estimate for normal mixture models with component specific variances. Computational Statistics & Data Analysis, 2003. DOI 10.1016/S0167-9473(02)00176-7.
B. Panic, J. Klemenc and M. Nagode. Improved initialization of the EM algorithm for mixture model parameter estimation. Mathematics, 2020. DOI 10.3390/math8030373.
R Core Team. R: A language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing, 2023. URL https://www.R-project.org/.
S. Rathnayake, G. McLachlan, D. Peel, et al. EMMIXmfa: Mixture models with component-wise factor analyzers. 2019.
L. Scrucca and A. E. Raftery. Improved initialisation of model-based clustering using Gaussian hierarchical partitions. Advances in data analysis and classification, 2015. DOI 10.1007/s11634-015-0220-z.
N. Shimizu and H. Kaneko. Direct inverse analysis based on Gaussian mixture regression for multiple objective variables in material design. Materials & Design, 2020. DOI 10.1016/j.matdes.2020.109168.
D. Xu and J. Knight. Continuous Empirical Characteristic Function Estimation of Mixtures of Normal Parameters. Econometric Reviews, 2010. DOI 10.1080/07474938.2011.520565.

References

Reuse

Text and figures are licensed under Creative Commons Attribution CC BY 4.0. The figures that have been reused from other sources don't fall under this license and can be recognized by a note in their caption: "Figure from ...".

Citation

For attribution, please cite this work as

Chassagnol, et al., "Gaussian Mixture Models in R", The R Journal, 2023

BibTeX citation

@article{RJ-2023-043,
  author = {Chassagnol, Bastien and Bichat, Antoine and Boudjeniba, Cheïma and Wuillemin, Pierre-Henri and Guedj, Mickaël and Gohel, David and Nuel, Gregory and Becht, Etienne},
  title = {Gaussian Mixture Models in R},
  journal = {The R Journal},
  year = {2023},
  note = {https://doi.org/10.32614/RJ-2023-043},
  doi = {10.32614/RJ-2023-043},
  volume = {15},
  issue = {2},
  issn = {2073-4859},
  pages = {56-76}
}

© The R Foundation, web page contact.